FACTORIELLE (ANALYSE)

FACTORIELLE (ANALYSE)

L’analyse factorielle est une méthode mathématique expérimentale, spécialement employée en psychologie, qui a pour objet l’étude des dimensions, ou facteurs , d’un domaine empirique donné.

Soit, par exemple, les mesures de longueur, de surface et de volume d’un ensemble de corps physiques. L’analyse factorielle de ces mesures découvre trois facteurs: la longueur, la hauteur et la profondeur. Toutes les variables de ce domaine sont fonction de ces trois dimensions ou facteurs. Toutefois, si ces notions rejoignent l’évidence descriptive dans les sciences de la nature, il n’en va pas de même dans beaucoup d’autres secteurs, et en particulier dans les sciences sociales et humaines. Dans ces dernières disciplines, on peut sans doute décrire un certain nombre de variables, mais il n’est guère possible, dans la plupart des cas, de déterminer les dimensions fondamentales de variation.

Considérons un autre exemple: l’intelligence. Bien qu’il s’agisse là d’un concept classique de la philosophie et de la psychologie, l’analyse rationnelle courante n’est pas en mesure de nous renseigner sur son unicité ou sa pluralité; en d’autres termes, elle ne peut pas nous apprendre si l’intelligence est une aptitude unitaire ni si, au contraire, ce qu’on désigne par ce vocable est constitué par une série d’aptitudes partielles; au cas où il en serait ainsi, elle ne peut dire dans quelle mesure ces dernières seraient indépendantes les unes des autres ou, au contraire, relativement intégrées. Élargissant le débat aux autres domaines de la psychologie, on pourrait se poser les mêmes questions au sujet de la mémoire, de la perception, de la stabilité émotionnelle, des attitudes politiques, de la structure des groupes humains, etc. On voit aisément que, si l’on dispose d’une méthode capable de déterminer avec précision les dimensions impliquées par ces concepts, ceux-ci deviendront plus rigoureux et les variables distinguées par la psychologie pourront être soumises à un contrôle plus discriminatif. Il n’échappe à personne que l’évaluation de l’intelligence par les tests, pour parler d’un domaine dont les conséquences individuelles et sociales sont immenses, ne saurait fournir des indications dignes de confiance que si les épreuves utilisées mettent en jeu des dimensions dont l’existence a été établie avec une probabilité suffisante.

L’analyse factorielle trouve son origine historique (1904) dans l’étude de l’intelligence et a été développée par C. Spearman, G. H. Thomson, C. Burt et L. L. Thurstone, qui en sont les fondateurs. Elle a été étendue par la suite à l’étude de la personnalité, et son emploi est actuellement très général. Elle s’applique dans tous les domaines de la psychologie et dans diverses autres disciplines (médecine, gestion, linguistique).

L’analyse factorielle consiste essentiellement en un ensemble de techniques mathématiques qui permettent d’analyser en plusieurs composantes fondamentales, scientifiquement interprétables, la variance d’un certain nombre de variables. Ces composantes, ou facteurs , sont en général linéaires. Elles expriment la communauté de variation entre les variables et peuvent être trouvées à partir des corrélations qui existent entre celles-ci. Le langage mathématique principal de l’analyse factorielle est l’algèbre matricielle. Celle-ci, qui figurait déjà implicitement dans les premiers travaux de Spearman parus au début de ce siècle, est devenue de plus en plus explicite dans les recherches ultérieures de Burt et surtout de Thurstone.

Les résultats acquis par l’analyse factorielle en ce qui concerne l’intelligence et la personnalité ont contribué à en faire une technique fondamentale de la psychométrie. Elle est indispensable dans l’établissement des diagnostics et pronostics requis par le classement, l’orientation et la sélection des sujets dans les principaux secteurs de l’activité humaine.

1. Les théories fondamentales

L’analyse factorielle est née en 1904 avec l’ouvrage où C. Spearman (1863-1945) consigna les résultats de ses premiers travaux: General Intelligence Objectively Determined and Measured. Les recherches de Spearman, auxquelles il faut associer celles de G. H. Thomson (1881-1955), caractérisent ce que l’on a appelé la période de l’analyse unifactorielle , du fait que les théories dominantes s’attachaient alors à expliquer l’intelligence par l’existence d’un seul facteur général.

Vers 1930 commence une seconde période, celle de l’analyse multifactorielle , représentée notamment par les travaux de C. Burt (1883-1971) et de L. L. Thurstone (1887-1955). À partir de ce moment, l’intérêt se déplace peu à peu du facteur général vers les facteurs multiples, d’abord pour ce qui concerne l’intelligence, ensuite à propos de tous les aspects du comportement.

On peut caractériser l’analyse factorielle: 1. par l’emploi de modèles mathématiques, surtout l’algèbre matricielle; 2. par le développement d’épreuves statistiques destinées à établir la significativité des résultats; 3. par la programmation des calculs en vue du traitement par les ordinateurs; 4. par l’extension de la méthode à tous les domaines de la psychologie (intelligence, aptitudes, tempérament, caractère, motivation, apprentissage, etc.) et à d’autres sciences (pédagogie, sociologie, anthropométrie, anthropologie, etc.). Son emploi est particulièrement fécond en psychologie différentielle et en psychologie appliquée, où elle permet de déterminer les dimensions du psychodiagnostic des études, des métiers, etc. Elle conduit en outre à élaborer des modèles théoriques se rapportant aux différences individuelles, à la pratique clinique, à l’orientation et à la sélection scolaire et professionnelle.

C. Spearman et le facteur g

L’hypothèse de Spearman peut être écrite comme suit:

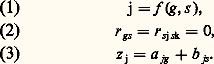Ces égalités signifient: qu’une activité cognitive quelconque j est fonction d’un facteur général , g , commun à toutes les activités, et d’un facteur spécifique , s , lequel n’est présent que dans cette activité (1); que tous les facteurs sont statistiquement indépendants, c’est-à-dire que leurs corrélations sont nulles (2); que la mesure z ^j d’un comportement j peut être écrite en première approximation comme une fonction linéaire de g et de s , c’est-à-dire qu’elle est composée d’une partie due au facteur g , représentée par le coefficient factoriel de j en g , a ^jg , augmentée d’une partie due au facteur spécifique s , représentée par le coefficient factoriel de j en s , b ^js (3).

De cette hypothèse, on peut déduire: a ) que toutes les corrélations entre tests cognitifs seront positives (r ^jk 礪 0), puisque g est commun, mais qu’elles ne seront pas parfaites (r ^jk 麗 1), puisque chaque s est spécifique et indépendant; b ) que la table de corrélations doit être hiérarchique ou, selon le langage matriciel, que le rang de la matrice de corrélations doit être égal à l’unité.

Pour clarifier ce dernier point, examinons le tableau 1. Il s’agit d’une matrice de corrélations, c’est-à-dire d’un ensemble de corrélations ordonnées par lignes et par colonnes. Supposons qu’elle ait été obtenue en appliquant quatre tests à un échantillon de sujets et en calculant les corrélations entre les résultats obtenus. On dit qu’une matrice est hiérarchique lorsque ses colonnes sont proportionnelles. Le tableau 1 est celui d’une matrice hiérarchique. Ainsi, pour les colonnes 2 et 3:

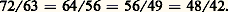Or, si l’hypothèse de Spearman est exacte, la corrélation partielle entre deux tests cognitifs quelconques doit être nulle:

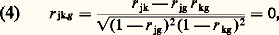La formule (4) exprime la corrélation qui subsiste entre j et k lorsque l’effet de g est éliminé. Donc, sa valeur doit être nulle, puisque, selon l’hypothèse de Spearman, g est le seul facteur commun. Mais (4) n’est nulle que si le numérateur est nul. Donc:

D’où la proportionnalité des colonnes. En effet, d’après (5), le rapport entre deux termes correspondants de deux colonnes doit être constant:

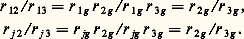On voit donc que, si l’hypothèse de Spearman est exacte, les corrélations doivent être positives et hiérarchiques. Dans nombre d’études, Spearman et ses collaborateurs ont cru confirmer ces prévisions.

Dans le cas d’une hiérarchie de tests, il est facile en principe de calculer le coefficient factoriel de chaque test en g. Ce coefficient est donné par:

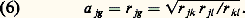En effet, si l’on opère la transformation de (5) en (6), on a:

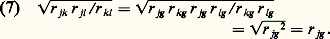Le coefficient factoriel du test 1 en g sera dès lors:

Les coefficients des tests en g figurent dans la colonne g du tableau 1, comme on peut le vérifier aisément en appliquant la formule (6).

On a interprété le facteur g en étudiant les coefficients factoriels d’un grand nombre de tests cognitifs différents qui répondaient à l’exigence de la hiérarchie. Spearman a montré que g correspond à l’abstraction noégénétique , c’est-à-dire à l’activité d’abstraction et de mise en relation qui fait surgir ( 塚﨎益﨎靖晴﨟) des nouvelles connaissances ( 益礼﨎晴益). D’après Spearman, toutes les opérations cognitives qui accroissent les connaissances sont identiques et se réduisent à la fonction d’abstraction et de mise en relation. Cette fonction se maintient à un niveau constant pour chaque sujet, puisque g est la mesure de l’énergie mentale ou, du point de vue somatique, de l’énergie nerveuse du sujet. Les facteurs spécifiques seraient les mécanismes par lesquels cette énergie agit.

Spearman en conclut que toutes les théories antérieures de l’intelligence sont erronées. Ainsi, les théories monarchiques , selon lesquelles l’intelligence est une faculté unique, négligent les facteurs s ; d’autre part, les théories anarchiques , selon lesquelles il n’y a pas d’intelligence mais seulement des comportements intelligents, ne prennent pas en considération le facteur g. Quant aux théories oligarchiques , qui prônent l’existence de plusieurs facultés, elles sont également dans l’erreur puisque les corrélations montrent qu’il n’y a pas d’ensembles distincts de corrélations, mais un seul ensemble hiérarchique, c’est-à-dire un seul facteur g en plus des facteurs spécifiques.

G. H. Thomson: facteurs et lois de probabilité

De son côté, Thomson offre une autre explication des corrélations positives et hiérarchiques: il s’agit de la théorie dite de l’échantillonnage. Supposons: a ) que l’intelligence soit un ensemble de N éléments e équivalents, indépendants et très nombreux; b ) qu’un test ou activité j soit un échantillon aléatoire , formé par un nombre Np ^j d’éléments de l’ensemble selon la complexité p ^j du test; c ) que la corrélation r ^jk entre deux tests j et k dépende du nombre d’éléments communs aux deux tests. On peut alors écrire: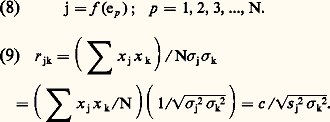

La formule habituelle de la corrélation (9) exprime le rapport entre la covariance c et la racine carrée du produit des variances. Mais la covariance indique le nombre d’éléments communs aux deux tests. Or, étant donné que chaque test est un échantillon aléatoire et indépendant et que les proportions d’éléments de chaque test sont p ^j et p ^k, le nombre le plus probable d’éléments communs dans les deux échantillons sera Np ^jp ^k. De même, la variance de chaque échantillon est représentée par son nombre d’éléments Np ^j et Np ^k. Donc, (9) devient:

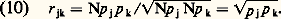À partir de (10), on peut montrer que les corrélations doivent être hiérarchiques. En effet, en prenant deux colonnes quelconques d’une table de corrélations, par exemple les colonnes 2 et 3, on a:

On voit que les colonnes sont proportionnelles comme dans la théorie de Spearman.

D’après la théorie de Thomson, l’intelligence n’est pas constituée de facultés ou de facteurs, mais d’un ensemble d’éléments. Ceux-ci seraient des constituants simples appartenant au substrat causal du comportement intelligent, liés sans doute au bagage génétique et, plus directement, aux dix milliards de neurones corticaux. Ils sont si nombreux que les lois de la probabilité peuvent y jouer et produire cette tendance remarquable qu’on appelle hiérarchie.

Spearman et Thomson se fondent l’un et l’autre sur le fait de la hiérarchie. Mais ce fait est discutable. Au fur et à mesure que les techniques psychométriques et les modèles d’échantillonnage s’améliorent et que les erreurs de tout genre diminuent, les corrélations s’éloignent de plus en plus de la hiérarchie. C’est d’ailleurs ce qui a amené Spearman à admettre l’existence d’autres facteurs communs à côté de g , et Thomson lui aussi a reconnu que l’ensemble des éléments n’est pas homogène, mais structuré en sous-ensembles partiels. Ainsi, l’interprétation unifactorielle est devenue peu à peu une interprétation multifactorielle. Celle-ci sera explicitement formulée par Burt et par Thurstone.

C. Burt: facteurs et classes

Les techniques de Burt et de Thurstone ont été incorporées, pour la plus grande partie, à la méthodologie de l’analyse factorielle. On tentera d’en faire la synthèse à la section suivante. On se borne à présenter ici les concepts théoriques les plus distinctifs de ces auteurs.

Étant donné que toutes les corrélations entre des tests cognitifs sont positives, il faut admettre, d’après Burt, l’existence d’un facteur général g. Toutefois, celui-ci ne suffit pas à expliquer les corrélations, puisqu’elles ne sont pas tout à fait hiérarchiques. Il faut donc admettre, en plus de g , d’autres facteurs qui, étant communs à plusieurs tests, ne sont ni communs à tous ni spécifiques d’un seul: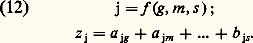

Chaque test peut être exprimé en fonction d’un facteur général g , de un ou de plusieurs facteurs communs m et d’un facteur spécifique s.

Burt a été l’un des auteurs les plus féconds dans le développement des méthodes factorielles; il a largement contribué à leur application dans la recherche en psychologie différentielle et en psychologie appliquée. D’après lui, les facteurs que l’on trouve ne sont pas des entités réelles, mais des catégories logiques et métriques de classification. Ces principes logico-métriques permettent de fonder une taxinomie des phénomènes psychologiques et des individus, au moyen de classes qui sont à la fois rigoureuses, indépendantes, objectives et empiriquement vérifiées.

L. L. Thurstone: facteurs et paramètres fonctionnels

C’est à Thurstone que revient le mérite d’avoir donné à l’analyse factorielle sa formulation la plus générale, et l’on peut affirmer que la théorie inclut les autres au titre de cas particuliers. Sa seule hypothèse est que chaque activité ou phénomène j est fonction d’un nombre de facteurs communs m , d’un facteur spécifique s et d’une erreur e :

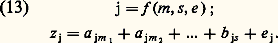Quant au nombre et à la nature des facteurs communs, c’est là un problème qui doit être résolu expérimentalement. Dans ce but, Thurstone a développé de nombreuses techniques sur le modèle général de l’algèbre matricielle. Ces techniques sont devenues la base de l’analyse factorielle. Les facteurs ainsi découverts sont interprétés comme des paramètres dans l’équation de chaque variable d’un domaine empirique donné. Ces paramètres correspondent à un ensemble de concepts théoriques en fonction desquels le domaine étudié peut être analysé de façon scientifiquement vérifiable. En général, les facteurs psychologiques représentent des principes fonctionnels et des traits.

2. La méthodologie

On peut distinguer dans une analyse factorielle quatre phases: la préparation, la factorisation, la rotation et l’interprétation.

La phase de préparation

L’analyse factorielle peut être une analyse d’exploration ou de vérification. Dans le premier cas, on ne dispose pas d’hypothèses préalables suffisamment précises. Dans l’analyse de vérification, on peut formuler à l’avance de telles hypothèses. De toute manière, la préparation de l’analyse est indispensable. Elle consiste à définir avec le plus de rigueur opérationnelle possible le domaine à étudier ou les hypothèses de départ ainsi que les conditions expérimentales capables de les éprouver: variables, tests, sujets, modèle mathématique, etc. Il est souhaitable que les variables choisies délimitent clairement au départ un domaine déterminé et, si des hypothèses ont déjà été formulées à son sujet, que chacune d’entre elles soit représentée par trois variables au moins. Si l’hypothèse est exacte, ces variables dépendront d’un certain facteur hypothétique, et non des autres. Les tests correspondants sont alors appliqués aux sujets et les corrélations calculées.

Supposons, par exemple, que l’on veuille étudier l’intelligence. Faisons en outre l’hypothèse qu’elle est régie par deux facteurs: le raisonnement et la mémoire. Il faudrait choisir et développer de nombreux tests pour mesurer toute une variété de comportements intelligents, parmi lesquels en figureraient plusieurs qui, par hypothèse, dépendraient du raisonnement et non de la mémoire, et inversement. Pour atteindre ce but, des centaines de tests seraient nécessaires. Afin de présenter clairement les principes de la méthode, réduisons ces tests aux six épreuves suivantes: 1. répétition d’idées; 2. répétition de chiffres; 3. problèmes arithmétiques; 4. répétition de mots; 5. syllogismes; 6. ordinations. Supposons qu’on ait appliqué ces tests à un échantillon convenable de sujets et qu’on ait calculé les corrélations. Ces dernières sont données dans les entrées latérales du tableau 2. Les valeurs de la diagonale principale traduisent les communautés des tests, dont on parlera par la suite.

La factorisation

La phase suivante consiste à trouver combien de facteurs communs sont nécessaires et suffisants pour expliquer les corrélations. Une représentation géométrique permet aisément de comprendre le problème. On peut démontrer que la matrice de corrélations du tableau 2 équivaut à la configuration vectorielle de la figure 1. La configuration est un ensemble de vecteurs qui représentent chacun un test. La longueur et la position de chaque vecteur sont déterminées par la matrice de corrélations.

Ainsi, à partir de la matrice de corrélations, on construit la configuration vectorielle. Le nombre de facteurs nécessaires pour expliquer les corrélations est le nombre de dimensions de l’espace défini par la configuration. Si cet espace est une ligne, on n’a besoin que d’un seul facteur. Tel était le sens de la théorie de Spearman. Mais, en général, il y a plusieurs dimensions. Si le nombre de celles-ci est plus grand que trois, on ne peut pas construire une configuration physique, mais on peut faire les calculs appropriés avec la même facilité. Dans le cas qui nous occupe (fig. 1), tous les vecteurs sont dans un plan. La configuration est donc à deux dimensions. Elle nous montre que les corrélations exigent deux facteurs.

On peut représenter chaque dimension par un axe de coordonnées, comme dans la figure 2. On a choisi un premier axe passant par le vecteur 1 et un second perpendiculaire au premier. L’ensemble des vecteurs et des axes constitue une structure. La figure 2 donne la structure factorielle de l’exemple choisi, avec six vecteurs (autant que de tests) et deux axes orthogonaux (autant que de facteurs). La structure de la figure 2 nous permet d’établir la matrice de factorisation (tabl. 3), dans laquelle les lignes représentent les tests ou vecteurs; les colonnes, les facteurs ou axes; et les valeurs, les coordonnées de chaque vecteur dans chaque axe.

La matrice du tableau 3 est le résultat de la factorisation. Elle exprime les six variables en fonction de deux facteurs communs. Elle indique que deux facteurs sont nécessaires et suffisants pour expliquer les corrélations empiriques.

En effet, l’équation (13) peut être écrite:

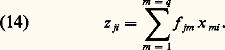L’équation (14) exprime l’hypothèse générale de l’analyse factorielle: la mesure d’une variable j dans un sujet i – que l’on va définir en échelle réduite pour simplifier le problème – est une fonction linéaire d’un nombre q de facteurs, exigés par la variable j selon les coefficients factoriels f ^jm et par le sujet i selon les cotes factorielles x ^mi .

En notation matricielle, (14) devient:

La matrice F ^t est d’ordre n.q , n étant le nombre de variables et q le nombre de facteurs. Elle constitue la matrice factorielle totale, dont chaque ligne indique la variance totale de chaque variable.

Cette matrice peut être définie comme la somme de deux matrices, la matrice factorielle commune F ^h , qui représente la partie de la variance due aux facteurs communs ou communauté :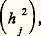

et la matrice factorielle unique F ^u , qui représente la partie due aux facteurs uniques ou unicité. Ainsi:

Mais la matrice de corrélations R formée par toutes les corrélations, comme en (9), est égale à:

On peut montrer par le calcul matriciel que:

L’équation (18) exprime un théorème fondamental de l’analyse factorielle: la matrice de corrélations empiriques avec les communautés de la diagonale principale est égale à la matrice factorielle commune postmultipliée par sa transposée.

Dans le cas d’une corrélation quelconque, l’équation (18) devient: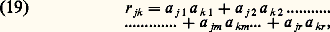

dans laquelle a ^jm est le coefficient factoriel de la variable j dans le facteur commun m et dans laquelle il y a r facteurs communs.

De même:

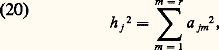ce qui signifie que la variance commune, ou communauté d’une variable j , est la somme des carrés de ses coefficients factoriels communs. Dès lors, si l’on considère une structure factorielle, comme celle de la figure 2, et si l’on prend deux vecteurs quelconques j et k , comme dans la figure 3, on voit que chaque vecteur j est l’hypoténuse d’un triangle rectangle dont les côtés sont les coefficients factoriels.

Donc, d’après (20):

On peut en conclure que la longueur d’un vecteur est la racine carrée de la communauté de la variable correspondante.

De même, d’après (19) et en remplaçant les coefficients a ^jm par leurs valeurs h ^j cos ^j 﨏 ^m :

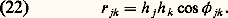L’équation (22) indique que la corrélation entre deux variables est égale au produit scalaire des deux vecteurs qui les représentent. À partir de (21) et de (22), on peut passer de la matrice empirique de corrélations à la configuration vectorielle et, de celle-ci, en introduisant les axes orthogonaux nécessaires, à la structure et à la matrice finale de factorisation.

La rotation

Dans la phase précédente, on a introduit le nombre nécessaire d’axes. Ce nombre est, à une erreur près, déterminé par les corrélations. Mais les axes peuvent être placés dans un nombre infini de positions. Leur position reste donc indéterminée. Celle qui leur est assignée dans la figure 2 est arbitraire. Elle répond à des critères exclusivement mathématiques qui permettent de découvrir combien d’axes sont nécessaires. Si l’on veut interpréter les facteurs, il s’agit maintenant de procéder à une rotation des axes vers une position qui soit en quelque sorte unique et surdéterminée. Le critère de la structure simple , proposé par Thurstone et développé mathématiquement par Tucker, Carroll, Kaiser et Saunders en particulier, un principe de rotation très employé. Il consiste à supposer que, dans le comportement humain, certains phénomènes ou activités dépendent électivement de certains principes ou paramètres. S’il en est ainsi et si, dans une recherche, on a réussi à représenter chaque paramètre par plusieurs variables, les vecteurs correspondants donneront une configuration simple. Ils ne figureront pas à un endroit quelconque de l’espace vectoriel, mais dans des sous-espaces ou hyperplans définis par le ou les paramètres dont ils sont fonction. Il y aura lieu d’opérer la rotation des axes de telle sorte que la position de chaque axe soit définie par la position de chaque hyperplan vectoriel. On appelle structure simple une structure formée par l’ensemble d’une configuration simple et des axes orthogonaux aux hyperplans.

Dans le cas qui nous occupe, il y avait deux dimensions. Il s’agit d’établir si les vecteurs sont contenus dans deux hyperplans à une dimension, c’est-à-dire dans deux droites. S’il en est ainsi, on doit opérer la rotation des axes pour les rendre perpendiculaires à ces deux lignes. La figure 4 donne le résultat de cette rotation.

L’interprétation

La structure simple de la figure 4 conduit à la matrice factorielle finale du tableau 4, avec les coordonnées des vecteurs dans les nouveaux axes. Chaque facteur peut être interprété d’après les coefficients des variables, puisque l’axe correspondant a été défini par des vecteurs empiriques. Ainsi, le facteur A est exigé par les tests 2 et 4 (répétition de chiffres et de mots). Il semble correspondre à la mémoire répétitive. Il est également présent, encore que de façon moins nette dans les tests 1 (répétition d’idées) et 6 (ordinations). L’interprétation semble donc être confirmée. Ces tests exigent aussi quelque effort de mémoire, mais ils sont moins mécaniques. Le facteur ne semble pas entraîner de différences individuelles dans les tests 3 et 5 (problèmes et syllogismes), ce qui confirme une fois de plus l’interprétation donnée. Le facteur B est interprété de la même façon et semble correspondre au raisonnement.

Quel que soit le critère de la factorisation et de la rotation, l’interprétation de chaque facteur doit expliquer pourquoi les coefficients factoriels sont élevés, moyens ou faibles dans les différents tests. Ces interprétations doivent servir comme hypothèses de départ pour de nouvelles expériences factorielles d’un type identique ou différent. De cette façon, les interprétations initiales peuvent être confirmées ou modifiées, voire rejetées. La valeur de chaque facteur dépend de son pouvoir explicatif à l’intérieur des analyses factorielles successives, de sa portée théorique générale compte tenu de l’ensemble des connaissances acquises et de son utilité sur le plan des prévisions pratiques.

La hiérarchie factorielle

La factorisation et la rotation, qui, naguère encore, exigeaient des mois d’effort et d’ingéniosité, sont effectuées en quelques minutes à l’aide de calculateurs électroniques. Les deux phases principales de l’analyse factorielle restent la préparation et l’interprétation. C’est à ce niveau que le psychologue et, en général, le chercheur doivent manifester leur créativité et leur rigueur. Le reste est devenu, heureusement, presque automatique. De plus, on a développé d’autres modèles d’analyse pour l’étude de données ordinales et qualitatives. Enfin, l’analyse factorielle n’est plus considérée comme une théorie psychologique, moins encore comme une théorie de l’intelligence. Elle est devenue une technique descriptive et expérimentale, avec ses possibilités et ses limites propres, et qui, correctement employée, peut fournir des informations précieuses, parfois exclusives, sur les dimensions de n’importe quel domaine de covariation.

En ce qui concerne les résultats de l’analyse factorielle, il suffit de signaler ici que, dans tous les domaines de la conduite humaine, on a trouvé: a ) qu’il y a de nombreux facteurs; b ) que ces facteurs ne sont pas simples et qu’une analyse plus fine découvre d’autres sous-facteurs; c ) qu’ils ne sont pas non plus indépendants, car l’analyse de leurs corrélations met en évidence d’autres facteurs plus généraux; d ) que l’ensemble de facteurs constitue une sorte de hiérarchie factorielle.

D’après l’analyse factorielle, la personnalité apparaît comme une structure hiérarchique à la fois unitaire , vu que les facteurs sont interdépendants, et complexe , en raison du grand nombre des facteurs; ordonnée , enfin, du fait que ces facteurs se situent à des niveaux différents de généralité.

Encyclopédie Universelle. 2012.